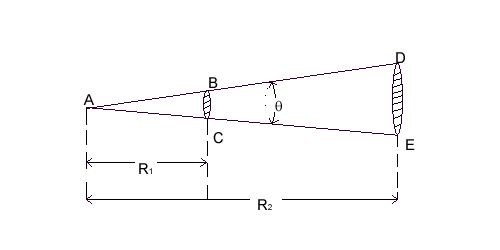
Figure 1: A sketch of the geometry used to scale the size of one object to another to determine distance.
OBJECT: This exercise is designed to determine the distance to the sun by a method of triangulation. The method relies on the geometry of proportional triangles.
INTRODUCTION
The use of scaling,
ratios and proportionality is a powerful tool for measurements. Indeed,
all measurements are made relative to a reference. An object is "more
of less" massive than another, one person is "younger or older" than another
and one distance is "longer or shorter than another.
The figure shown below shows
how we can use triangles to scale the distance to an object whose size
in known.

Consider the two triangles, ABC and ADE to see how we can scale distances. When linear and angular distances are compared there is a simple relationship between the two that states:
The distance BC = R1(distance)q(in radians) EQUATION 1
and
The distance DE = R2(distance)q(in radians) EQUATION 2
Solving for q in each case and equating "things equal to the same thing are equal to each other."
Then:
BC/R1=DE/R2 EQUATION 3
The distance to the object at greater distance is given by:
R2=(DE/BC)R1
EQUATION 4
DISTANCE TO THE SUN
The sun subtends an arc of 32.5" at a location from the earth. If we know the size of the sun, we can calculate the distance to the sun as follows:
The radius of the Sun is known to be 6.96X10^5 Km
Using equation 2, the distance to the sun, R2 is given by:
R2=(solar radius)/(angle in radians)
R2=2X6.96X10^5 Km/(32.5'/60'/degree)(2*Pi*radians/360degrees)
R2=13.92X10^5 Km/(9.44X10^-3)
R2=1.472X10^8 Km or in miles 8.98X10^7 miles
This becomes the "true value"
of the distance to the sun for comparison with the value that you determine.
You will use this to calculate the %error from the equation given later
in this exercise.
PROCEDURE
Take the projection tube that is constructed using a pin hole in one end and a projection screen attached to the other as shown in the sketch below.
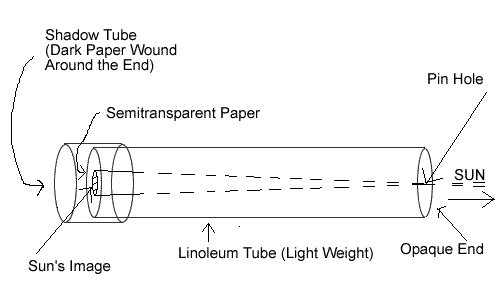
Aim the tube at the sun and
align it so that the pin hole is toward the sun and the projection screen
can be seen by you clearly. Project the sun's image onto the end
toward your eyes. When the image is displayed alongside the marked
metric tape measure the size across the disk of the sun. Now measure
the length of the tube from the pin hole to the display screen to get one
side of a smaller triangle. Record the measurements in the table
provided. You should make about four or five measurements to get
a good average for the calculations. Complete the table entries and
the calculations shown in each column.
| LENGTH | IMAGE SIZE | ANGLE (RADIANS) | DISTANCE (KM) | % ERROR |
To calculate the percent error, average the distances in the fourth column and put the average in the following equation.
% error = ((True Value - Observed Value)/True
Value)*100%
SUMMARY
When you have completed this
special exercise, you have conducted a very important scientific observation
that can be used as a tool for future work.
Let us assume that all galaxies
are 100,000LY across. If you look at a galaxy through your projection
device and observe that the image of a galaxy is 0.001 arc seconds across
in size, how far away is the galaxy? You really need to have a telescope
to do this, but let us image such a result.
You have really made a "break
through" with the measurement of the distance to a galaxy.
How far away is the moon from
the earth? The angle subtended at the eye or the image projected
on the projection screen is about the same size as that of the sun.
Try to project the moon at a night when it is full and bright and see what
you get. The radius of the moon is 1738 KM.
The distances to the moon
at the two extremes are:
At apogee 406,000KM
At perigee 363,000KM
This exercise was prepared by Dr. Jim Roberts for use in physics 1050 and physics 1060 to earn extra credit points 11/8/1999
This exercise was adapted for the web by Timothy
Imholt 6/2001.